gravitation class 10 question and answer | Class 10 Science Chapter 1 Gravitation Exercise Question 1.
Study the entries in the following table and rewrite them putting the connected items in a single row :
| I | II | III |
| Mass | m/s2 | Zero at the centre of the earth |
| Weight | kg | Measure of inertia |
| Acceleration due to gravity | N.m2/kg2 | Same in the entire universe |
| Gravitational constant | N | Depends on height |
Answer:
| I | II | III |
| Mass | kg | Measure of inertia |
| Weight | N | Depends on height |
| Acceleration due to gravity | m/s2 | Zero at the centre of the earth |
| Gravitational constant | N.m2/kg2 | Same in the entire universe |
Gravitation Class 10 Maharashtra Board Question 2.
Answer the following questions.
(a) What is the difference between mass and weight of an object? Will the mass and weight of an object on the earth be the same as their values on Mars? Why?
Answer:
The mass of an object is the amount of matter present in it. It is same everywhere in the Universe and is never zero. It is a scalar quantity and its SI unit is kg. The weight of an object is the force with which the earth (or any other planet/ moon/star) attracts it. It is directed towards the centre of the earth. The weight of an object is different at different places on the earth. It is zero at the earth’s centre. It is a vector quantity and its SI unit is the newton (N). The magnitude of weight = mg.
The mass of an object will be the same on the earth and Mars, but the weight will not be the same because the value of g on Mars is different from that on the earth.
(b) what are (i) free fall, (ii) acceleration due to gravity (iii) escape velocity (iv) centripetal force?
Answer:
(i) Free fall:
Whenever an object moves under the influence of the force of gravity alone, it is said to be falling freely.
(ii) Acceleration due to gravity:
The acceleration produced in a body due to the gravitational force of the earth is called the acceleration due to gravity.
[Note: On the earth’s surface, the value of the acceleration due to gravity is almost uniform. If a body falls from a low altitude, the value of the acceleration due to gravity is almost the same.]
(iii) Escape velocity:
When a body is thrown vertically upward from the surface of the earth, the minimum initial velocity of the body for which the body is able to overcome the downward pull by the earth and can escape the earth forever is called the escape velocity.
(iv) Centripetal force:
In uniform circular motion of a body, the force acting on the body is directed towards the centre of the circle. This force is called centripetal force.
(c) Write the three laws given by Kepler. How did they help Newton to arrive at the inverse square law of gravity?
Kepler’s first law :
The orbit of a planet is an ellipse with the Sun at one of the foci.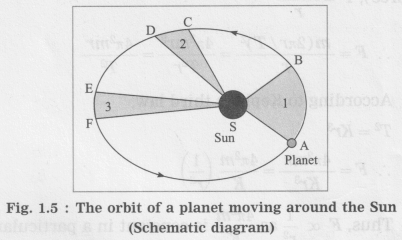
Figure 1.5 shows the elliptical orbit of a planet revolving around the Sun (S).
Kepler’s second law :
The line joining the planet and the Sun sweeps equal areas in equal intervals of time.
A → B, C → D and E → F are the displacements of the planet in equal intervals of time.
The straight lines AS, CS and ES sweep equal areas in equal intervals of time.
Area ASB = area CSD = area ESF.
Kepler’s third law :
The square of the period of revolution of a planet around the Sun is directly proportional to the cube of the mean distance of the planet from the Sun.
Thus, if r is the average distance of the planet from the Sun and T is its period of revolution, then,
T2 ∝ r2, i.e.,
For simplicity, we shall assume the orbit to be a circle.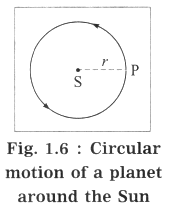
In Fig. 1.6,
S denotes the position of the Sun, P denotes the position of a planet at a given instant and r denotes the radius of the orbit (= the distance of the planet from the Sun). Here, the speed of the planet is uniform.
If m is the mass of the planet, the centripetal force exerted on the planet by the Sun (= gravitational force),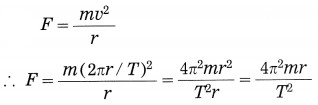
According to Kepler’s third law,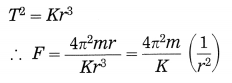
Thus, F ∝
(d) A stone thrown vertically upwards with initial velocity u reaches a height ‘h’ before coming down. Show that the time taken to go up is same as the time taken to come down.
Answer: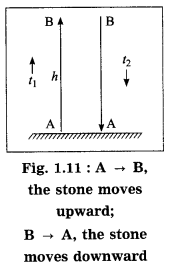
We have, v = u + at …..(1)
and s = ut +
∴ s = (v – at) t +
= vt – at2 +
∴ s = vt –
As the stone moves upward from A → B,
s = AB = h, t = t1,
a = -g (retardation),
u = u and v = 0
∴ From Eq. (3), h = 0 –
∴ h =
As the stone moves downward from B → A,
t = t2, u = 0, s = h and a = g
∴ from Eq. (2), h =
From Eqs. (4) and (5), t12 = t22
∴ t1 = t2 (∵ t1 and t2 are positive)
(e) If the value of g suddenly becomes twice its value, it will become two times more difficult to pull a heavy object along the floor. Why?
Answer:
To pull an object along the floor, it is necessary to do work against the force of friction between the object and the surface of the floor. This force of friction is proportional to the weight, mg, of the object. If the value of g becomes twice its value, the weight of the object and hence the force of friction will become double. Therefore, it will become two times more difficult to pull a heavy object along the floor.
10th Gravitation Chapter Exercise Question 3.
Explain why the value of g is zero at the centre of the earth.
The value of g changes while going deep inside the earth. It goes on decreasing as we go from the earth’s surface towards the earth’s centre.
We shall treat the earth as a sphere of uniform density. If we consider a particle of mass m at point P at a distance (R – d) from the earth’s centre, where R is the radius of the earth and d is the depth below the earth’s surface, the gravitational force on the particle due to the earth is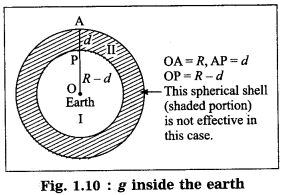
F = 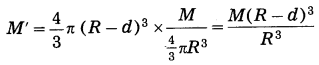
because the outer spherical shell is not effective (Fig. 1.10). In this case, the acceleration due to gravity is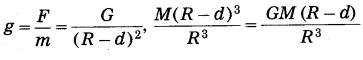
where M is the mass of the earth. Thus, g decreases as d increases. It is less than that at the earth’s surface (
∴ g = 0.
[Note : The formulae given in the answer are not given in the textbook. The formula density =
Let the period of revolution of a planet at a distance R from a star be T. Prove that if it was at a distance of 2R from the star, its period of revolution will be 8–√T .
Answer:T=
For r = R, T =T1.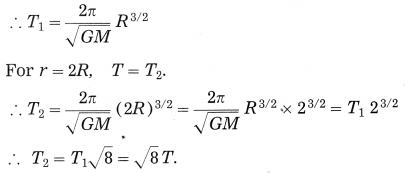
Class 10 Science 1 Chapter 1 Gravitation Question 5.
Solve the following examples.
(a) An object takes 5 s to reach the ground from a height of 5 m on a planet. What is the value of g on the planet?
Solution:
Data: u = 0 m/s, s = 5m, t = 5s, g = ?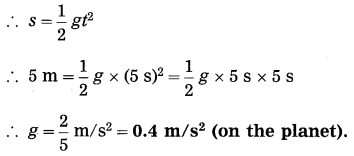
Data : RA = RB/2, gB = 
Data: m = 5 kg, W = 49 N,
gM =
(i) The mass of the object on the moon = the mass of the object on the earth = 5 kg
(ii) W = mg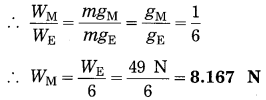
(weight of the object on the moon).
(d) An object thrown vertically upwards reaches a height of 500 m. what was its initial velocity? How long will the object take to come back to the earth? Assume g = 10 m/s2
(e) A ball falls off a table and reaches the ground in 1 s. Assuming g = 10 m/s2, calculate its speed on reaching the ground and the height of the table.
Solution:
Data: t = 1s, g = 10 m/s2, u = 0 m/s,
s = ?, v = ?
(i) s = ut +
=
∴ s =
=5 m
∴ The height of the table = 5 m.
(ii) v = u +at = u + gt
= 0 m/s + 10 m/s2 × 1 s
= 10m/s
∴ The velocity of the ball on reaching the ground = 10 m/s.
(f) The masses of the earth and moon are 6 × 1024 kg and 7.4 × 1022 kg, respectively. The distance between them is 3.84 × 105 km. Calculate the gravitational force of attraction between the two. Use G = 6.7 × 10-11 N.m2 kg-2.
Solution:
Data : m1 = 6 × 1024 kg,
m2 = 7.4 × 1022 kg,
r = 3.84 × 105 km = 3.84 × 108 m,
G = 6.7 × 10-11 N.m2 kg-2, F = ?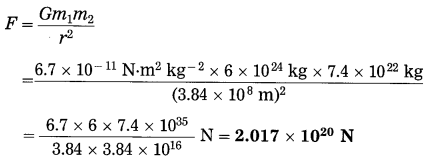
This is (the magnitude of) the gravitational force between the earth and the moon.
(g) The mass of the earth is 6 × 1024 kg. The distance between the earth and the Sun is 1.5 × 1011 m. If the gravitational force between the two is 3.5 × 1022 N, what is the mass of the Sun? (Use G = 6.7 × 10-11 N.m2 kg-2)
Solution:
Data : m1 = 6 × 1024 kg,
r = 1.5 × 1011 m, F = 3.5 × 1022 N,
G = 6.7 × 10-11 N.m2kg-2, m2 = ?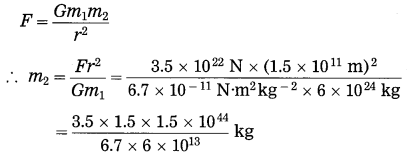
= 1.96 × 1030 kg (mass of the sun)
Gravitation Class 10 Exercise Answers Project:
Take weights of five of your friends. Find out what their weights will be on the moon and the Mars.
Answer:
Help: The weight of a body
(i) On the earth. W1 = mg1
(ii) on the moon, W2 = mg2
(iii) on Mars, W3 = mg3
∴ W2 = W1 ×
Now, g1 = 9.81 m/s2, g2 = 1.67 m/s2 and g3 = 3.72 m/s2
If W1 = 500 N,
W2 = 500 ×
and W3 = 500 ×
Can you recall? (Text Book Page No. 1)
10th Class Science Part 1 Chapter 1 Gravitation Exercise Question 1.
What are the effects of a force acting on an object? (Note: a body ≡ an object)
Answer:
- A force can set a body in motion. For example, if a ball at rest on the floor is pushed, it rolls on the floor.
- A force can stop a moving body. For example, a moving bicycle can be brought to rest by application of brakes.
- A force acting on a body can change the speed of the body. For example, when brakes are applied to a moving bicycle, its speed decreases due to the friction between the brake shoes and the rim of the tire.
- A force can change the direction of motion of the body. For example, in a uniform circular motion of a body, the direction of motion of the body keeps on changing due to the applied force.
- A force can change the speed as well as the direction of motion of the body. For example, when a ba ll bowled by a bowler is hit by a batsman, there occurs a*change in the speed as well as the direction of motion of the ball.
- A force can change the shape and size of the body on which it acts. For example, when a rubber ball is pressed, it gets deformed and hence no longer remains spherical. Also, there can be a decrease in its volume.
1 Gravitation Exercise Question 2.
What types of forces are you familiar with?
Answer:
The gravitational force between the earth and the moon, the electromagnetic force between two charged particles in motion, the nuclear force between a proton and a neutron in the nucleus of an atom.
Gravitation 10th Class Exercise Question 3.
What do you know about the gravitational force?
Answer:
The gravitational force is a universal force, i.e., it acts between any two objects in the universe.
Can you recall? (Text Book Page No. 1)
Science Part 1 Gravitation Exercise Question 1.
What are Newton’s laws of motion?
Answer:
(1) Newton’s first law of motion: An object continues to remain at rest or in a state of uniform motion along a straight line unless an external unbalanced force acts on it.
(2) Newton’s second law of motion: The rate of change of momentum is proportional to the applied force and the change of momentum occurs in the direction of the force.
(3) Newton’s third law of motion: Every action force has an equal and opposite reaction force that acts simultaneously.
[Note: Equal in magnitude and opposite in direction.]
Use your brainpower! (Text Book Page No. 4)
10th Sciece Part 1 Gravitation Exercise Question 1.
If area ESF in figure 1.5 is equal to area ASB, what will you infer about EF?
Answer:
The time taken by the planet to move from E to F equals the time taken by the planet to move from A to B.
Use your brainpower (Text Book Page No. 7)
Gravitation Exercise 10th Class Question 1.
According to Newton’s law of gravitation, every object attracts every other object.
Thus, if the earth attracts an apple towards itself, the apple also attracts the earth towards itself with the same force. Why then does the apple fall towards the earth, but the earth does not move towards the apple?
Answer:
The earth and the apple move towards each other, but the magnitude of the displacement of the earth is negligible relative to that of the apple. Also the observer is located on the earth.
[Note: The mass of the earth is far greater than that of an apple. Hence, the magnitude of the acceleration of the earth is negligible relative to that of the apple.]
Gravitation Class 10 Question And Answer Question 2.
The gravitational force due to the earth also acts on the moon because of which it revolves around the earth. Similar situation exists for the artificial satellites orbiting the earth. The moon and the artificial satellites orbit the earth. The earth attracts them towards itself but unlike the falling apple, they do not fall on the earth, why?
Answer:
This is because of the velocity of the moon and the satellites along their orbits. If this velocity was not there, they would have fallen on the earth.
Think about it (Text Book Page No. 8)
Std 10 Science Chapter 1 Gravitation Exercise Question 1.
What would happen if there were no gravity?
Answer:
There would be no gravitational attraction between any two particles and hence no formation of the solar system, galaxy, etc.
Science 1 Gravitation Question 2.
What would happen if the value of G was twice as large?
Answer:
The gravitational force between any two particles would become double, also the value of g would become double.
Can you tell? (Text Book Page No. 8)
Gravitation Class 10 Exercise Question 1.
What would be the value of g on the surface of the earth if its mass was twice as large and its radius half of what it is now? (March 2019)
Answer:
∴ g2 = 8g1
Thus, the value of g on the surface of the earth would be eight times the present value.
Think about it (Text Book Page No. 9)
Std 10 Science Chapter 1 Gravitation Answers Question 1.
Will the direction of the gravitational force change as we go inside the earth?
Answer:
No.
Gravitation Class 11 Exercise Solutions State Board Question 2.
What will be the value of g at the centre of the earth?
Answer:
Zero.
Use your brain power! (Text Book Page No. 10)
10th Ssc Science Chapter 1 Gravitation Question 1.
Will your weight remain constant as you go above the surface of the earth?
Answer:
No. As we go above the surface of the earth, our weight will go on decreasing.
Class 10 Science Chapter 1 Gravitation Question 2.
Suppose you are standing on a tall ladder. If your distance from the centre of the earth is 2R, what will be your weight?
Answer:![]()
= 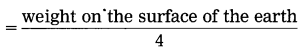
Use your brain power! (Text Book Page No. 12)
Gravitation Class 11 Maharashtra Board Question 1.
According to Newton’s law of gravitation, the earth’s gravitational force is higher on an object of larger mass. Why doesn’t that object fall down with higher velocity as compared to an object with lower mass?
Answer:
F = ma and F =
∴ Acceleration, a =
Use your brain power! (Text Book Page No. 6)
Question 1. Assuming the acceleration in Example 2 above remains constant, how long will Mahendra take to move 1 cm towards Virat?
Answer:
Here, u = 0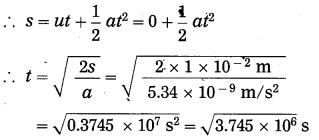
= 1935 s = 32 minutes 15 seconds.
Fill in the blanks with appropriate words and write the completed sentences :
Question 1. The ratio g(earth)/g(moon) is equal to……..
Answer:
The ratio g(earth)/g(moon) is equal to 6 (approximately)
Question 2. The value of the acceleration due to gravity……..as we move from the equator to a pole.
Answer:
The value of the acceleration due to gravity increases as we move from the equator to a pole.
Question 3. If the earth shrinks to half of its radius, its mass remaining the same, the weight of an object on the earth will become……..times.
Answer:
If the earth shrinks to half of its radius, its mass remaining the same, the weight of an object on the earth will become four times.
Question 4. The SI unit of weight is the……..
Answer:
The SI unit of weight is the newton.
Question 5. The CGS unit of weight is the……..
Answer:
The CGS unit of weight is the dyne
Question 6. The weight of a body is ……..at the poles.
Answer:
The weight of a body is maximum at the poles.
Question 7. Outside the earth, the weight of a body varies as……..
Answer:
Outside the earth, the weight of a body varies as 1/(R + h)2
Question 8. Due to the …….. force, the earth attracts all objects towards it.
Answer:
Due to the gravitational force, the earth attracts all objects towards it. Gravitational
Question 9. The acceleration due to gravity does not depend on the …….. of the body.
Answer:
The acceleration due to gravity does not depend on the mass of the body. Mass
Question 10. According to Kepler’s first law, the orbit of a planet is …….. with the Sun at one of the……..
Answer:
According to Kepler’s first law, the orbit of a planet is an ellipse with the Sun at one of the foci
Question 11. According to Kepler’s second law, the line joining the planet and the Sun …….. in equal intervals of time.
Answer:
According to Kepler’s second law, the line joining the planet and the Sun Sweeps equal areas in equal intervals of time.
Question 12. According to Kepler’s third law T2 ∝ rn, where n = ……..
Answer:
According to Kepler’s third law T2 ∝ rn, where n = 3
Question 13. For a freely falling object, we can write Newton’s second equation of motion as ……..
Answer:
For a freely falling object, we can write Newton’s second equation of motion as S =
Question 1.
(A) Write the proper answer in the square. (Practice Activity Sheet – 1)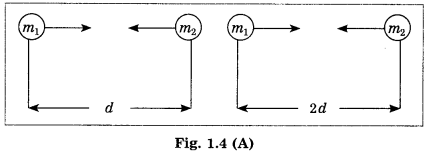
If this F = x
Then F =
Answer:
F = 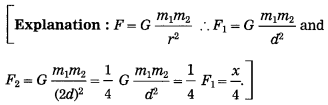
(B) Write the proper answer in the square. (March 2019)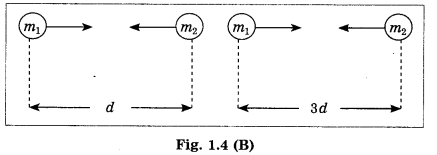
If F =
then F =
Answer:
F =
Choose the correct alternative and rewrite the statements:
Question 1. The gravitational force between two particles separated by a distance r varies as ……..
(a)
(b) r
(c) r2
(d)
Answer:
(d)
Question 2. In the usual notation, the acceleration due to gravity at a height h from the surface of the earth is ……..
Answer:
(c) g =
Question 3. The SI unit of the universal constant of gravitation is ……..
(a) N.m2/kg2
(b) N.kg2/m2
(c) m/s2
(d) kg.m/s2
Answer:
(a) N.m2/kg2
Question 4. The escape velocity of a body from the earth’s surface, vsec = …….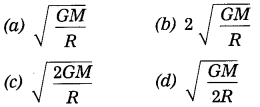
Answer:
(c)
Question 5.
How much will a person with 72 N weight on the earth, weigh on the moon? (Practice Activity Sheet-1)
(a) 12 N
(b) 36 N
(c) 21 N
(d) 63 N
Answer:
(a) 12 N
Question 6.
What will be the weight of a person on the earth, who weighs 9N on the moon? (Practice Activity Sheet – 2)
(a) 3 N
(b) 15 N
(c) 45 N
(d) 54 N
Answer:
(d) 54 N
State whether the following statements are True or False : (If a statement is false, correct it and rewrite it.)
Question 1.
If the separation between two particles is doubled, the gravitational force between the particles becomes half the initial force.
Answer:
False. (If the separation between two particles is doubled, the gravitational force between the particles becomes
Question 2.
The CGS unit of the universal constant or gravitation is the dyne cm2/gram2?
Answer:
True.
Question 3.
At the centre of the earth, the value of the acceleration due to gravity becomes zero.
Answer:
True.
Question 4.
The weight of a body is minimum at the poles.
Answer:
False. (The weight of a body is maximum at the poles.)
Question 5.
Mass is a vector quantity.
Answer:
False. (Mass is a scalar quantity.)
Question 6.
weight is a vector quantity.
Answer:
True.
Question 7.
g has maximum value at the equator.
Answer:
False. (g has maximum value at the poles.)
Question 8.
Outside the earth, g varies as 1/(R + h)2.
Answer:
True.
Question 9.
The value of G changes from place to place.
Answer:
False. (The value of G is the same throughout the universe.)
Question 10.
The value of g increases with altitude.
Answer:
False. (The value of g decreases with altitude.)
Question 11.
The escape velocity of a body does not depend on the mass of the body.
Answer:
True
Question 12.
The mass of a body is the amount of matter present in it.
Answer:
True
Match the following :
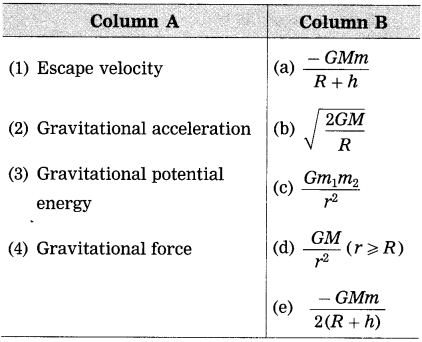
Answer:
(1) Escape velocity :
(2) Gravitational acceleration :
(3) Gravitational potential energy :
(4) Gravitational force :
Answer the following questions in one sentence each:
Question 1.
State the SI and CGS units of G.
Answer:
The SI unit of G is N.m2/kg2 and CGS unit is the dyne.cm2/g2.
Question 2.
State any one characteristic of gravitational force.
Answer:
Gravitational force between two particles does not depend on the nature of the medium between them.
Question 3.
Name the force that keeps a satellite in the orbit around the earth.
Answer:
The gravitational force due to the earth keeps a satellite in the orbit around the earth.
Question 4.
Name the force due to which the earth revolves around the Sun.
Answer:
The earth revolves around the Sun due to the gravitational force of attraction exerted on it by the Sun.
Question 5.
What is the acceleration due to gravity at a height h ( = radius of the earth) from the surface of the earth? (g = 9.8 m/s2)
Answer:
The acceleration due to gravity at a height h ( = radius of the earth) from the surface of the earth is 2.45 m/s2.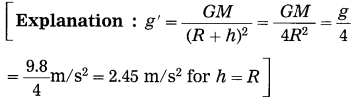
Question 6.
What is the relation between the SI unit of weight and the CGS unit of weight?
Answer:
The relation between the SI unit of weight (the newton) and the CGS unit of weight (the dyne) is 1 newton = 105 dynes.
Question 7.
Write the formula for the centripetal force acting on a body performing circular motion.
Answer:
F =
Question 8.
Write the formula for the escape velocity of a body from the earth’s surface.
Answer: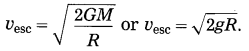
Question 9.
What is the value of the acceleration due to gravity at the centre of the earth?
Answer:
Zero.
Question 10.
What are the factors on which the maximum height attained by a body thrown upwards depends?
Answer:
The initial velocity of the body, the acceleration due to gravity at that place, the buoyant force and frictional force due to air.
Some of the important terms in chapter Gravitation are given in the following box. Find them :

Answer:
(1) centripetal force
(2) escape velocity
(3) periodic time
(4) gravitational constant.
Answer the following questions:
Question 1.
What is centripetal force?
(OR)
Define centripetal force.
Answer:
In uniform circular motion of a body, the force acting on the body is directed towards the centre of the circle. This force is called centripetal force.
Question 2.
Give one example of centripetal force.
Answer:
The moon revolves around the earth due to the gravitational force exerted on it by the earth. This force is directed towards the centre of the earth and is thus a centripetal force.
Question 3.
Name the source responsible for the motion of a planet around the Sun.
Answer:
A planet revolves around the Sun due to the gravitational force exerted on it by the Sun.
Answer the following questions:
Question 1.
In the following figure, an orbit of a planet around the Sun (S) has been shown. AB and CD are the distances covered by the planet in equal time. Lines AS ad CS sweep equal areas in equal intervals of time. Hence, areas ASB and CSD are equal. (Practice Activity Sheet-1)
(a) Which laws do we understand from the above description?
(b) Write the law regarding the area swept.
(c) Write the law T2 ∝ r3 in your words.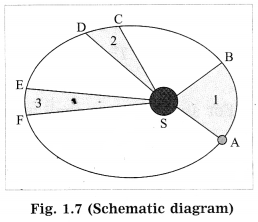
Answer:
(a) From the given description we understand Kepler’s three laws.
(b) Kepler’s law of areas: The line joining the planet and the Sun sweeps equal areas in equal intervals of time.
(c) Kepler’s law of periods: The square of the period of revolution of a planet around the Sun is directly proportional to the cube of the mean distance of the planet from the Sun.
Question 2.
Identify the law shown in Fig. 1.7 and state the three respective laws. (Practice Activity Sheet – 3)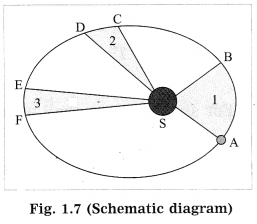
Answer:
(a) From the given description we understand Kepler’s three laws.
(b) Kepler’s law of areas: The line joining the planet and the Sun sweeps equal areas in equal intervals of time.
(c) Kepler’s law of periods: The square of the period of revolution or a planet around the Sun is directly proportional to the cube of the mean distance of the planet from the Sun.
Question 3.
Explain the term gravitational force. What is gravitation?
Answer:
There exists a force of attraction between any two particles of matter in the universe such that the force depends only on the masses of the particles and the separation between them. It is called the gravitational force and the mutual attraction is called gravitation.
Question 4.
State Newton’s universal law of gravitation. Express it in mathematical form.
Answer:
Newton’s universal law of gravitation :
Every object in the Universe attracts every other object with a definite force. This force is directly proportional to the product of the masses of the two objects and inversely proportional to the square of the distance between them.
Mathematical form: Consider two objects of masses m1 and m2. We assume that the objects are very small spheres of uniform density and the distance r between their centers is very large compared to the radii of the spheres (Fig. 1.8).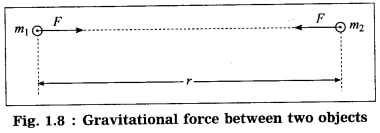
The magnitude (F) of the gravitational force of attraction between the objects is directly proportional to m1m2 and inversely proportional to r2
∴ F ∝
∴ F =
where G is the constant of proportionality, called the universal gravitational constant.
[Note: In the textbook, the word object/body is used.
Newton’s law of gravitation applies to particles.]
Question 5.
(i) Why is the constant of gravitation called a universal constant?
(ii) Newton’s law of gravitation is called the universal law of gravitation. Why?
Answer:
(i) The value of the constant of gravitation does not change with the nature, mass or the size of the material particles. It does not vary with the distance between the two particles. It is also independent of the nature of the medium between the two particles. Hence, it is called a universal constant.
(ii) As the law of gravitation given by Newton is applicable throughout the universe and to all particles, it is called universal law.
[ Note: The centre of mass of an object is the point inside or outside the object at which the total mass of the object can be assumed to be concentrated to study the effect of an applied force. The centre of mass of a spherical object having uniform density is at its geometrical centre. The centre of mass of an object having uniform density is at its centroid. If the two bodies are spherical and of uniform density, the gravitational force between them is always along the line joining the centres of the two bodies and the distance between the centres is taken to be r. When the bodies are not spherical or have irregular shape or have nonuniform density, the force is along the line joining their centres of mass and r is taken to be the distance between the two centres of mass.]
Question 6.
If the distance between two bodies is increased by a factor of 5, (i) by what factor will the gravitational force change if the masses are kept constant? (ii) by what factor will the mass of one of them have to be altered, keeping the other mass the same, to maintain the same gravitational force between the two bodies?
Answer:
If the distance between two bodies is increased by a factor of 5,
(i) the gravitational force between the bodies will decrease by a factor of 25 if the masses of the bodies are kept constant.
(ii) the mass of one of them will have to be increased by a factor of 25, keeping the mass of the other body the same, to maintain the same gravitational force between the two bodies.
[Note : Gravitational force F ∝
Question 7.
(i) Determine the SI unit of the universal constant of gravitation from the formula for the gravitational force between two particles. Hence, state the CGS unit of the constant of gravitation. (ii) Define G (universal gravitational constant).
Ans. (i) According to Newton’s law of gravitation, the gravitational force between two particles is
F =
where m1 and m2 are the masses of the two particles, r is the distance between them and G is the universal constant of gravitation.
∴ G =
The SI unit of force is the newton (N), that of distance is the metre (m) and that of mass is the kilogram (kg).
The SI unit of G is
The CGS unit of G is
(ii) F =
∴ G =
If we take m1 = m2 = unit mass and r = unit distance, numerically, G = F, i.e., G (universal gravitational constant) represents the magnitude of the gravitational force of attraction between two unit masses, separated by a unit distance.
Question 8.
State the importance of Newton’s universal law of gravitation.
Answer:
The importance of Newton’s universal law of gravitation :
This law explains successfully, i.e., with great accuracy,
- The force that binds the objects on the earth to the earth
- The motion of the moon and artificial satellites around the earth
- The motion of the planets, asteroids, comets, etc., around the Sun
- The tides of the sea due to the moon and the Sun.
Question 9.
Compare the gravitational force on a body of mass 1 kg due to the earth with the force on the same body due to another body of mass 1 kg at a distance of 1 m from the first body. (Mass of the earth = 6 × 1024 kg, radius of the earth = 6400 km)
Answer:
In the first case, m1 = 1kg,
m2 = 6 × 1024 kg and r = 6400 km = 6.4 × 106 m
The gravitational force on the body.![]()
=
In second case, m1 = 1 kg
m2 = 1 kg and r = 1m
Gravitational force on the body,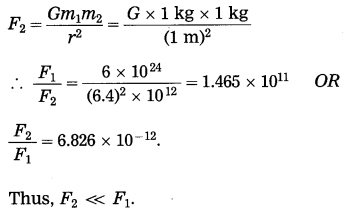
Question 10.
Explain the term the earth’s gravitational force.
(OR)
Write a short note on the earth’s gravitational force.
Answer:
The earth attracts every object towards it because of the gravitational force. As the earth’s centre of mass is at its centre, the gravitational force exerted by the earth on an object is directed towards the earth’s centre. Hence, an object released from a point above the earth’s surface falls vertically downward towards the earth.
If an object is thrown vertically upward, its velocity goes on decreasing due to the earth’s gravitational force on the object. At one stage, the velocity of the body becomes zero and later the body falls back to the earth.
Question 11.
Take two balls of different masses, go to the top of a building, drop them simultaneously and observe what happens to the balls.
Answer:
The balls reach the ground almost at the same time.
Question 12.
Take two similar pages from your notebook. Crumple one paper and allow this and the other paper to fall on the ground simultaneously. What do you observe?
Answer:
The crumpled paper reaches the ground before the other one.
Question 13.
Take a feather and a paper. Allow them to fall to the ground simultaneously. Which will reach the ground earlier? Why?
Answer:
There is no unique answer. It depends on the feather and paper. Upthrust due to air and force due to friction with air play very important roles here. The acceleration of a body depends on the resultant of the earth’s gravitational force on the body and the upthrust and the force of friction due to air.
Question 14.
From Newton’s law of gravitation, derive the formula for the acceleration due to gravity.
Answer:
Suppose that a body of mass m is released from a distance r from the centre (O) of the earth (Fig. 1.9). Let M be the mass of the earth. According to Newton’s law of gravitation, the magnitude of the earth’s gravitational force acting on the body Is
F = G
where G is the universal constant of gravitation.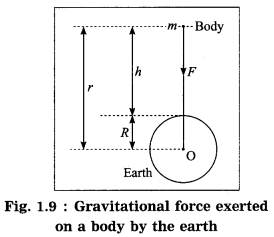
The acceleration produced by this force, force F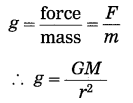
This is the formula for the acceleration due to gravity or the gravitational acceleration due to the earth. This acceleration is directed towards the earth’s centre.
If h denotes the altitude, r = R + h, where R is the radius of the earth.
∴ g =
For a body on the earth’s surface, h = 0 ∴ g =
[Note: When we consider the gravitational interaction between the earth and a body on the surface of the earth or at some height above the surface of the earth, for many practical purposes we can assume that the earth behaves as if its mass were concentrated at the earth’s centre. The proof is not expected here.]
Question 15.
Explain the factors affecting the value of g.
Answer:
The value of the acceleration due to gravity, g, changes from place to place on the earth. It also varies with the altitude and depth below the earth’s surface. The factors affecting the’ value of g are the shape of the earth, altitude and depth below the earth’s surface.
(1) The earth is not perfectly spherical. It is somewhat flat at the poles and bulging at the equator. At the surface of the earth, the value of g is maximum (9.832 m/s2) at the poles as the polar radius is minimum, while it is minimum (9.78 m/s2) at the equator as the equatorial radius is maximum.
(2) As the height (h) above the earth’s surface increases, the value of g decreases. It varies as
(3) In the interior of the earth, on average, the value of g is less than that at the earth’s surface. As the depth below the earth’s surface increases, the value of g decreases and finally it becomes zero at the centre of the earth.
Question 16.
If g = GM/r2, then where will the value^ of g be high, at Goa Beach or on the top of the Mount Everest? (Practice Activity Sheet – 3)
Answer:
The value of g will be high at Goa Beach.
Question 17.
Why does an object released from the hand, fall on the earth?
Answer:
When an object is held in the hand, the gravitational force acting on the object due to the earth is balanced by the person holding the object. When the object is released from the hand, it falls on the earth due to the earth’s gravitational force.
Question 18.
Does the value of g depend on the mass of the falling body? Why?
Answer:
The value of g does not depend on the mass of the falling body.
The reason is the gravitational force on a body due to the earth is directly proportional to the mass of the body and for a given force, the acceleration of a body is inversely proportional to the mass of the body.
Question 19.
Define mass. State its SI and CGS units.
Answer:
The mass of a body is the amount of matter present in it. Its SI unit is the kilogram (kg) and CGS unit is the gram (g).
[Note: Mass has only magnitude, not direction. Thus, it is a scalar quantity.]
Question 20.
Define weight. State its SI and CGS units.
Answer:
The weight of a body is defined as the force with which the earth attracts it. Its SI unit is the newton and CGS unit is the dyne.
[Note : In the usual notation, the magnitude of the weight of a body on the earth s surface is W =
Question 21.
As per the request of one of his friends from the equator, Rahul buys 100 grams of silver at the north pole. He hands it over to his friend at the equator. Will the friend agree with the weight of the silver bought? If not, why?
Answer:
The weight of a body is given by W = mg, where m is the mass of the body and g is the acceleration due to gravity, g varies from place to place. The value of g at the equator is less than that at the north pole (as well as the south pole). Hence, the weight of the silver bought at the north pole would be less when the silver is weighed at the equator. Therefore, Rahul’s friend will disagree about the weight of the silver.
[Note: The mass being independent of the value of g, Rahul’s friends will agree about the mass of the silver.]
Question 22.
What is the difference between mass and weight of an object? Will the mass and weight of an object on the earth be the same as their values on Mars? Why?
Answer:
The mass of an object is the amount of matter present in it. It is same everywhere in the Universe and is never zero. It is a scalar quantity and its SI unit is kg. The weight of an object is the force with which the earth (or any other planet/ moon/star) attracts it. It is directed towards the centre of the earth. The weight of an object is different at different places on the earth. It is zero at the earth’s centre. It is a vector quantity and its SI unit is the newton (N). The magnitude of weight = mg.
The mass of an object will be the same on the earth and Mars, but the weight will not be the same because the value of g on Mars is different from that on the earth.
Question 23.
Explain the term free fall and state the corresponding kinematical equations of motion in the usual notation.
Answer:
When a body falls in air, there are three forces acting on the body : (1) the gravitational force due to the earth, acting downward (2) the force of buoyancy (upthrust) due to air, acting upward I (3) the force due to friction with air (called air resistance), acting upward (being always in the direction opposite to that of the velocity of the body).
Under certain conditions, the force of buoyancy due to air and friction with air can be ignored compared to the gravitational force of the earth. In that case (near the earth’s surface) the body falls with almost uniform acceleration (g). Whenever a body moves under the influence of the force of gravity alone, it is said to be falling freely. Strictly speaking, this is true only if the body falls in vacuum.
The kinematical equations of motion, in the usual i notation, are
v = u + gt, s = ut +
If the initial velocity (u) of the body is zero,
v = gt, s =
Question 24.
During a free fall, will a heavier object accelerate more than a lighter one?
Answer:
No. The two objects will have the same acceleration.
Question 25.
If you had to calculate the mass of the earth, how would you do it?
Answer:
If the acceleration due to gravity (g), the constant of gravitation (G) and the radius of the earth (R) are known, the mass of the earth (M) can be calculated using the formula g =
Question 26.
What is gravitational potential energy?
(OR)
Define gravitational potential energy.
Write the formula for it.
Answer:
The energy stored in a body due to the gravitational force between the body and the earth is called the gravitational potential energy.
Gravitational potential energy of a body of mass m =
[Note : As the body is bound to the earth due to the earth’s gravitational froce, the gravitational potential energy of the body is negative. If the body is given kinetic energy equal to
Question 27.
What is escape Velocity?
(OR)
Define escape velocity.
Answer:
When a body is thrown vertically upward from the surface of the earth, the minimum initial velocity of the body for which the body is able to overcome the downward pull by the earth and can escape the earth forever is called the escape velocity.
Question 28.
Explain the term escape velocity.
(OR)
Write a short note on escape velocity.
Answer:
In general, when a body is thrown vertically upward from the earth’s surface, its velocity goes on decreasing and after some time the body falls back to the ground. If its initial velocity is increased, the maximum height attained by it is more, but it does fall back to the ground. If the initial velocity is increased continuously, for a particular initial velocity, the body can overcome the earth’s gravitational force and move to infinity and come to rest there. This velocity is called the escape velocity.
Question 29.
Using the law of conservation of energy, obtain the expression for the escape velocity.
Answer:
Here, we shall not consider the effects of air. Suppose a body of mass m is thrown vertically upward from the surface of the earth. Let the initial velocity of the body be the escape velocity (vsec).
When the body is on the earth’s surface, its total energy Ex = kinetic energy + potential energy =
Thus, E1 =
When the body moves to infinity and comes to rest there, its total energy,![]()
According to the law of conservation of energy,
E1 = E2.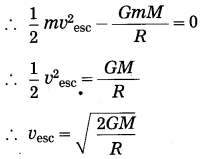
This is the required expression.
Question 30.
Express escape velocity in terms of g and R.
Answer:
Escape velocity, vesc =
Now, g =
∴ GM = gR2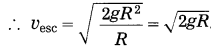
Question 31.
Express escape velocity in terms of G, R and ρ (the earth’s density)
Answer:
Give scientific reasons:
Question 1.
If a feather and a stone are released from the top of a building simultaneously, the stone reaches the ground earlier than the feather.
Answer:
(a) The motion of a body falling in air accelerated due to the earth’s gravitational force on the body. The force due to buoyancy of air acts on the body in the upward direction. As the body falls, the friction with air opposes its motion.
(b) This opposition due to air depends on the size, shape, density and velocity of the body. It Is greater for a feather than for a stone. Hence, the stone has greater downward acceleration than the feather. Therefore, the stone reaches the ground earlier than the feather though ‘they are released simultaneously from the same height.
Question 2.
The weight of a body is different on different planets.
Answer:
(1) The weight of a body of mass m on the surface of a planet of mass M and radius R is
W =
(2) For a given body, its mass is constant. G is the universal constant of gravitation. Different planets have different masses and radii such that the ratio (M/R2) is not the same. Hence, the weight of a body is different on different planets.
Question 3.
With a specific initial velocity, we can jump higher on the moon than on the earth.
Answer:
The acceleration due to gravity on the moon is about
Distinguish between the following:
Question 1.
mass and weight (2) universal gravitational constant and gravitational acceleration of the earth.
Answer:
(1) Mass:
- The mass of a body is the amount of matter present in it.
- It has magnitude, but not direction.
- It does not change from place to place.
- It can never be zero.
- Its SI unit is the kilogram.
Weight:
- The weight of a body is the force with which the earth attracts it.
- It has both magnitude and direction.
- It changes from place to place.
- It is zero at the centre of the earth.
- Its SI unit is the newton.
Question 2.
Universal gravitational constant:
- The universal gravitational constant numerically equals the force of attraction masses separated by a unit distance.
- Its value remains constant throughout the universe.
- It has magnitude but not direction.
- Its SI unit is N.m2/kg2.
Gravitational acceleration of the earth:
- The gravitational between two unit acceleration of the earth is the acceleration produced in a body due to the gravitational force of the earth.
- Its value changes from place to place.
- It has both magnitude and direction.
- Its SI unit is m/s2
Solve the following examples/numerical problems:
(G 6.67 × 10-11 N.m2/kg2, g = 9.8 m/s2)
Question 1.
The time taken by the earth to complete one revolution around the Sun is 3.156 × 107 s. The distance between the earth and the Sun is 1.5 × 1011 m. Find the speed of revolution of the earth.
Solution:
Data : T = 3.156 × 107 s,
r = 1.5 × 1011 m, v =?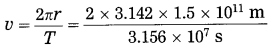
= 2.987 × 104 m/s = 29.87 km/s
This is the speed of revolution of the earth.
Question 2.
Assuming that the earth performs uniform circular motion around the Sun, flnd the centripetal acceleration of the earth. [Speed of the earth =3 × 104 m/s, distance between the earth and the Sun = 1.5 × 1011 m]
Solution:
Data: v = 3 × 104 m/s, r=1.5 × 1011 m
Centripetal force =
∴ Centripetal acceleration of the earth,![]()
= 6 × 10-3 m/s2
It is directed towards the centre of the Sun.
Question 3.
What will be the gravitational force on 60 kg man on the Moon, Mars and Jupiter? Are they the same? Why?
M (Moon) = 7.36 × 1022 kg, R (Moon) = 1.74 × 106m,
M (Mars) = 6.4 × 1023 kg, R (Mars) = 3.395 × 106 m,
M (Jupiter) = 1.9 × 1027 kg.
R (Jupiter) = 7.15 × 107 m,
G = 6.67 × 10-11 N.m/kg2
Solution:
(1) Data : m1 = 60 kg, m2 = 7.36 × 1022 kg,
R = 1.74 × 106 m, F = ?
= 97.29 N
On the moon’s surface, the gravitational force on the man due to the moon = 97.29 N.
(2) Data : m1 = 60 kg, m2 = 6.4 × 1023 kg,
R = 3.395 × 106m, F = ?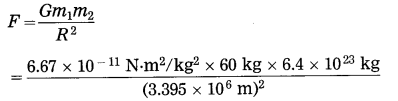
= 222.2 N
On the surface of Mars, the gravitational force on the man due to Mars = 222.2 N.
(3) Data : m1 = 60 kg, m2 = 1.9 × 1027 kg,
R = 7.15 × 107 m, F = ?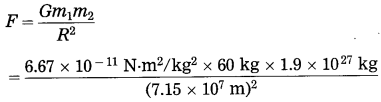
= 1487 N
On the surface of Jupiter, the gravitational force on the man due to Jupiter = 1487 N.
Thus, the forces on the man are not the same because the ratio (M/R2) is not the same in the case of the moon, Mars, and Jupiter.
Question 4.
Mahendra and Virat are sitting at a distance of 1 meter from each other. Their masses are 75 kg and 80 kg respectively. What is the gravitational force between them? G = 6.67 × 10-11 N.m2/kg2. (Practice Activity Sheet – 3)
Solution:
Given: r = 1 m,
m1 = 75 kg,
m2 = 80 kg
G = 6.67 × 10-11 N.m2/kg2![]()
= 4.002 × 10-7 N
The gravitational force between Mahendra and Virat is 4.002 × 10-7 N.
Question 5.
Spheres A and B of uniform density have masses 1 kg and 100 kg respectively. Their centres are separated by 100 m. (i) Find the gravitational force between them, (ii) Find the gravitational force on A due to the earth, (iii) Suppose A and B are initially at rest and A can move freely towards B. What will be the velocity of A one second after it starts moving towards B? How will this velocity change with time? How much time will A take to move towards B by 1 cm? (iv) if A begins to fall, starting from rest, due to the earth’s downward pull, what will be its velocity after one second? How much time will it take to fall through 1cm?
[M(earth) = 6 × 1024 kg, R(earth) = 6400 km]
Solution:Data: m1 = 1 kg, m2 = 100 kg, r = 100 m,
M =6 × 1024 kg,
R = 64o0 km = 6400 × 103 m,
t = 1 s, s = 1 cm = 1 × 10-2 m,
G = 6.67 × 10-11 N.m2/kg
F1 =?, F2 =?, v1 =?, t1 =?, v2 =?, t1 =?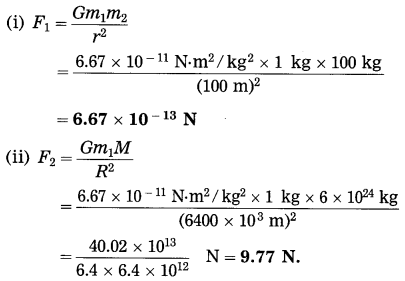
This is far greater than F1.
(iii) Ignoring variation of acceleration with distance,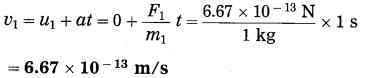
This velocity is directed from A to B. As the separation between A and B decreases, the acceleration of A and hence the velocity of A will increase.
Ignoring variation of acceleration with distance,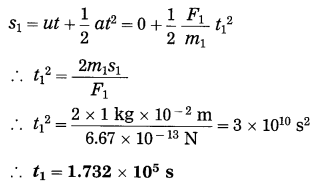
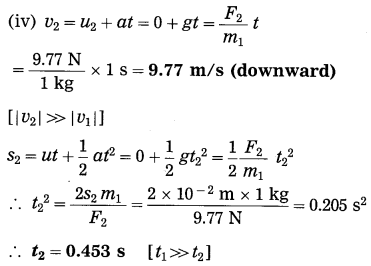
Question 6.
Two spheres of uniform density have masses 10 kg and 40 kg. The distance between the centres of the spheres is 200 m. Find the gravitational force between them.
Solution:
Data: m1 = 10 kg, m2 = 40 kg,
r = 200 m, G = 6.67 × 10-11 N.m2/kg2, F = ?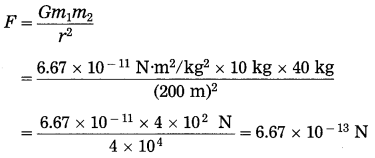
The gravitational force between the two spheres = 6.67 × 10-13 N.
Question 7.
Find the gravitational force between a man of mass 50 kg and a car of mass 1500 kg separated by 10 m.
Solution: Data : m1 = 50 kg, m2 = 1500 kg,
r = 10 m, G = 6.67 × 10-11 N.m2/kg2, F = ?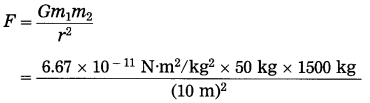
= 5.0025 × 10-8 N
The gravitational force between the man and the car = 5.0025 × 10-8 N.
Question 8.
Find the magnitude of the gravitational force between the Sun and the earth. (Mass of the Sun = 2 × 1024 kg, mass of the earth=6 × 1024 kg and the thstance between the centres of the Sun and the earth 1.5 × 1011 m,
G = 6.67 × 10-11 N.m2/kg2)
Solution:
Data: m1 = 2 × 1030 kg,
m2 = 6 × 1024 kg, r = 1.5 × 1011 m,
G = 6.67 × 10-11 N.m2/kg2, F =?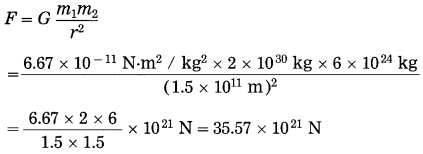
∴ F = 3.557 × 1022 N
The magnitude of the gravitational force between the Sun and the earth = 3.557 × 1022 N.
Question 9.
Find the magnitude of the acceleration due to gravity at the surface of the earth. (M= 6 × 1024 kg, R = 6400 km)
Solution:
Data: M = 6 × 1024 kg,
R = 6400km = 6.4 × 106m,
G = 6.67 × 10-11 N.m2/kg2, g =?
g = 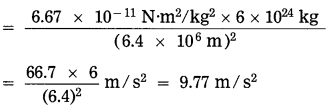
The magnitude of the acceleration due to gravity at the surface of the earth = 9.77 m/s2.
Question 10.
The mass of an imaginary planet is 3 times the mass of the earth. Its diameter is 25600 km arid the earth’s diameter is 12800 km. Find the acceleration due to gravity at the surface of the planet, [g (earth) = 9.8 m/s2]
Solution:
Data:
D1 (earth) = 12800 km
g1 (earth) = 9.5 m/s2, g2 (planet) = ?
The acceleration due to gravity at the surface of the planet = 7.35 m/s2.
Question 11.
If the acceleration due to gravity on the surface of the earth is 9.8 m/s2, what will be the acceleration due to gravity on the surface of a planet whose mass and radius both are two times the corresponding quantities for the earth?
Solution:
Data: ge = 9.8 m/s2, Mp = 2Me,
Rp = 2Re, gp = ?
Acceleration due to gravity, g = 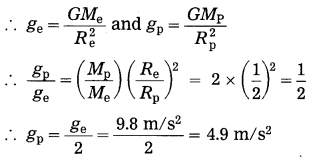
acceleration due to gravity on the surface of the planet = 4.9 m/s2.
Question 12.
A body is released from the top of a building of height 19.6 m. Find the velocity with which the body hits the ground.
Solution:
Data: h = 19.6 m, u = 0 m/s,
g = 9.8 m/s2, s = 19.6 m, v = ?
v2 = u2 + 2 gs .
=2 gs …..(as u = 0 m/s)
= 2 × 9.8 m/s2 × 19.6 m
= (19.6 m/s)2
∴ v = 19.6 m/s (downward velocity)
The velocity with which the body hits the i ground = 19.6 m/s (downward).
Question 13.
A stone on a bridge on a river falls into the river. If it takes 3 seconds to reach the surface of water, find (i) the velocity of the stone at the instant it touches the surface of water (ii) the height of the bridge from the surface of water.
Solution:
Data: u = 0 m/s, t = 3 s,
g = 9.8 m/s2, v = ?, h = ?
(i) v = u + gt = 0 m/s + 9.8 m/s2 × 3 s
= 29.4 m/s
The velocity of the stone at the instant it touches the surface of water = 29.4 m/s
(ii) s = ut +
= 0 m/s × 3 s +
= 4.9 × 9 m = 44.1 m
∴ The height of the bridge from the surface of water = 44.1 m.
Question 14.
A stone is dropped from rest from the top of a building 44.1 m high. It takes 3 s to reach the ground. Use this information to 1 calculate g.
Solution:
Data: u = 0 m/s, h = 44.1 m
∴ s = 44.1 m, t = 3 s, g =?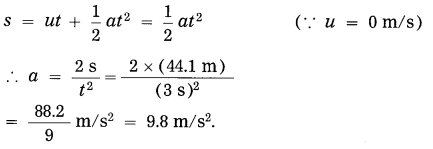
It is the acceleration due to gravity.
g = 9.8 m/s2.
Question 15.
A metal ball of mass 5 kg falls from a height of 490 m. How much time will it take to reach the ground? (g = 9.8 m/s2) (March 2019)
Solution:
Data: s = 490 m, a = g = 9.8 m/s2,
u = 0 m/s, s = ut +
∴ 490 = 0 × t +
∴ t2 =
∴ t = 10 s This is the required time.
Question 16.
If the weight of a body on the surface of the moon is 100 N, what is its mass? (g = 1.63 m/s2)
Solution:
Data: W= 100 N, g = 1.63 m/s2, m = ?
∴ W = mg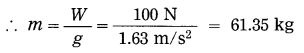
∴ The mass of the body = 61.35 kg.
Question 17.
A 100 kg bag of wheat is placed on a plank of wood. What is the weight of the bag and what is the reaction force exerted by the plank?
Solution:
Data: m = 100 kg, g = 9.8 m/s2,
W = ?, reaction force = ?
Magnitude of the weight,
W = mg = 100 kg × 9.8 m/s2 = 980 N
The weight of the bag = 980 N acting downward.
The reaction force exerted by the plank on the bag = 980 N acting upward.
Question 18.
Find the gravitational potential energy of a body of mass 10 kg when it is on the earth’s surface. [M(earth) = 6 × 1024 kg, it(earth) = 6.4 × 106m, G = 6.67 × 10-11 N. m2/kg2]
Solution:
Data: m = 10 kg, M = 6 × 1024 kg,
R = 6.4 × 106 m, G = 6.67 × 10-11 N.m2/kg2
The gravitational potential energy of the body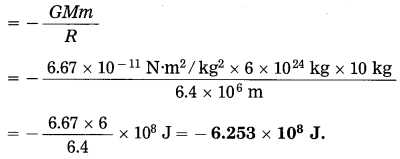
Question 19.
If the body in Ex. (26) performs uniform circular motion around the earth at a height of 3600 km from the earth’s surface, what will be its gravitational potential energy?
Solution:
Here, h = 3600 km = 3.6 × 106 m
∴ The gravitational potential energy of the body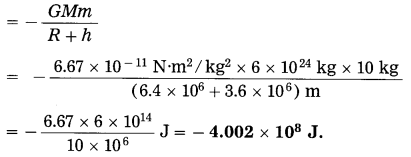
Question 20.
A body of mass 20 kg is at rest on the earth’s surface, (i) Find its gravitational potential energy, (ii) Find the kinetic energy to be provided to the body to make it free from the gravitational influence of the earth. (g = 9.8 m/s2, R = 6400 km)
Solution:
Data : m = 20 kg, g = 9.8 m/s2,
R = 6400 km = 6.4 × 106 m
(i) The gravitational potential energy of the body =
= – 20 kg × 9.8 m/s2 × 6.4 × 106 m
= – 1.2544 × 109 J.
(ii) To make the body free from the gravitational influence of the earth, it should be provided kinetic energy equal to 1.2544 × 109 J.
Question 21.
If the body in Ex. (28) is moving at 100 m/s on-the earth’s surface, what will be its (i) kinetic energy (ii) total energy?
Solution:
Data : m = 20 kg, u = 100 m/s .
(i) The kinetic energy of the body
=
(ii) The total energy of the body = kinetic energy + potential energy = 105 J + (- 1.2544 × 109 J)
= (1 – 12544) × 105 J = – 12543 × 105 J
= – 1.2543 × 109 J.
Question 22.
A satellite of mass 100 kg performs uniform circular motion around the earth at a height of 6400 km from the earth’s surface. Find its gravitational potential energy. [g = 9.8 m/s2, R = 6400 km]
Solution:
Data: m = 100 kg, g = 9.8 m/s2,
R = 6400 km = 6.4 × 106 m, h = 6.4 × 106 m
The gravitational potential energy of the satellite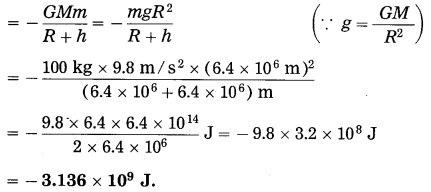
Question 23.
Find the escape velocity of a body from the earth. [M(earth) = 6 × 1024 kg, R (earth) = 6.4 × 106 m, G = 6.67 × 10-11 N.m2/ kg2]
Solution:
Data: M = 6 × 1024 kg, R = 6.4 × 106 m,
G = 6.67 × 10-11 N.m2/kg2
The escape velocity of a body from the earth,
Question 24.
Find the escape velocity of a body from the earth. [R (earth) = 6.4 × 106 m, ρ(earth) = 5.52 × 103 kg/m3, G = 6.67 × 10-11 N.m2/kg2]
Solution:
Data: R = 6.4 × 106 m, ρ = 5.52 × 103 kg/ m3, G = 6.67 × 10-11 N.m2/kg2
The escape velocity of a body from the earth
Question 25.
Calculate the escape velocity of a body from the moon. [g(moon) = 1.67 m/s2, R(moon) = 1.74 × 106 m]
Solution:
Data: g = 1.67 m/s2, R = 1.74 × 106 m
The escape velocity of a body from the moon,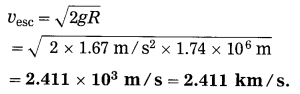
Question 26.
The mass of (an imaginary) planet is four times that of the earth and its radius is double the rathus of the earth. The escape velocity of a body from the earth is 11.2 × 103 mn/s. Find the escape velocity or a body from the planet.
Solution:
Data: M2 = 4M1, R2 = 2R1,
This is the escape velocity or a body from the planet.
Numerical Problems For Practice
[G = 6.67 × 1O-11 N.m2/kg2, mass or the earth =6 × 1024 kg, radius or the earthe 6.4 × 106 m]
Question 1.
A satellite of mass 1000 kg revolves around the earth in a circular path. If the distance between the satellite and the centre of the earth is 40000 km, find the gravitational force exerted on the satellite by the earth.
Answer:
250.1 N
Question 2.
The masses of two spheres are 10 kg and 20 kg respectively. If the distance between their centers is 100 m, find the magnitude of the gravitational force between them.
Answer:
1.334 × 10-12 N)
Question 3.
A satellite revolves around the earth along a circular path. If the mass of the satellite is 1000 kg and its distance from the center of the earth is 20000 km, find the magnitude of the earth’s gravitational force acting on the satellite.
Answer:
1000.5
Question 4.
Find the acceleration due to gravity at a distance of 20000 km from the center of the earth.
Answer:
1.0 m/s2
Question 5.
What is the weight of a body of mass 100 kg at the south pole? (g = 9.832 m/s2)
Answer:
983.2 N (downward)
Question 6.
What is the weight of a body of mass 20 kg at the equator? (g = 9.78 m/s2)
Answer:
195.6 N (downward)
Question 7.
A body is released from the top of a tower of height 50 m. Find the velocity with which the body hits the ground, (g = 9.8 m/s2)
Answer:
31.3 m/s (downward)
Question 8.
A body is thrown vertically upward with a velocity of 9.8 m/s. Calculate the maximum height attained by the body. (g = 9.8 m/s2)
Answer:
4.9 m
Question 9.
A particle of mass 10-6 kg performs uniform circular motion. Its period is 10 s and the radius of the circle is 2 m. Find (i) the speed of the particle (ii) the centripetal acceleration of the particle (iii) the centripetal force on the particle.
Answer:
(i) 1.257 m/s
(ii) 0.79 m/s2
(iii) 7.9 × 10-7 N
Question 10.
Find the gravitational potential energy of a body of mass 200 kg on the earth’s surface. [M(earth) = 6 × 1024 kg, R(earth) = 6400 km]
Answer:
-1.251 × 1010J
Question 11.
Find the gravitational potential energy of a body of mass 10 kg when it is at a height of 6400 km from the earth’s surface. [Given: a mass of the earth and radius of the earth. See Ex. 10 above.]
Answer:
-3.127 × 108 J
Question 12.
Find the escape velocity of a body from the moon.
[M(moon) = 7.36 × 1022 kg, R(moon) = 1.74 × 106 m]
Answer:
2.375 km/s
1. Gravitation
1. What are the effects of a force acting on an object?
2. What types of forces are you familiar with?
3. What do you know about the gravitational force?
We have seen in the previous standard that the gravitational force is a universal force and it acts not only between two objects on the earth but also between any two objects in the universe. Let us now learn how this force was discovered.
gravitation class 10 question and answer | Class 10 Science Chapter 1 Gravitation Exercise Question 1.
Gravitation
As we have learnt, the phenomenon of gravitation was discovered by Sir Isaac Newton. As the story goes, he discovered the force by seeing an apple fall from a tree on the ground. He wondered why all apples fall vertically downward and not at an angle to the vertical. Why do they not fly off in a horizontal direction? After much thought, he came to the conclusion that the earth must be attracting the apple towards itself and this attractive force must be directed towards the center of the earth.
The direction from the apple on the tree to the center of the earth is the vertical direction at the position of the apple and thus, the apple falls vertically downwards. Figure 1.1 on the left shows an apple tree on the earth. The force on an apple on the tree is towards the center of the earth i.e. along the perpendicular from the position of the apple to the surface of the earth. The Figure also shows the gravitational force between the earth and the moon.
The distances in the figure are not according to scale. Ø Gravitation Ø Circular motion and centripetal force Ø Kepler’s laws Ø Newton’s universal law of gravitation Ø Acceleration due to the gravitational force of the Earth Ø Free fall Ø Escape velocity Newton thought that if the force of gravitation acts on apples on the tree at different heights from the surface of the earth, can it also act on objects at even greater heights, much farther away from the earth, like for example, the moon? Can it act on even farther objects like the other planets and the Sun?
Force and Motion
We have seen that a force is necessary to change the speed as well as the direction of motion of an object.
Tie a stone to one end of a string. Take the other end in your hand and rotate the string so that the stone moves along a circle as shown in figure 1.2 a. Are you applying any force on the stone? In which direction is this force acting? How will you stop this force from acting? What will be the effect on the stone? As long as we are holding the string, we are pulling the stone towards us i.e. towards the centre of the circle and are applying a force towards it. The force stops acting if we release the string.
In this case, the stone will fly off along a straight line which is the tangent to the circle at the position of the stone when the string is released, because that is the direction of its velocity at that instant of time (Figure 1.2 b). You may recall that we have performed a similar activity previously in which a 5 rupee coin kept on a rotating circular disk flies off the disk along the tangent to the disk. Thus, a force acts on any object moving along a circle and it is directed towards the centre of the circle. This is called the Centripetal force. ‘Centripetal’ means centre seeking, i.e. the object tries to go towards the centre of the circle because of this force.
You know that the moon, which is the natural satellite of the earth, goes round it in a definite orbit. The direction of motion of the moon as well as its speed constantly changes during this motion. Do you think some force is constantly acting on the moon? What must be the direction of this force? How would its motion have been if no such force acted on it? Do the other planets in the solar system revolve around the Sun in a similar fashion?
Is similar force acting on them? What must be its direction? From the above activity, example and questions it is clear that for the moon to go around the earth, there must be a force which is exerted on the moon and this force must be exerted by the earth which attracts the moon towards itself. Similarly, the Sun must be attracting the planets, including the earth, towards itself.
Kepler’s Laws
Planetary motion had been observed by astronomers since ancient times. Before Galileo, all observations of the planet’s positions were made with naked eyes. By the 16th century a lot of data were available about planetary positions and motion. Johannes Kepler, studied these data. He noticed that the motion of planets follows certain laws. He stated three laws describing planetary motion. These are known as Kepler’s laws which are given below.
Kepler’s first law : The orbit of a planet is an ellipse with the Sun at one of the foci.
Kepler’s second law :The line joining the planet and the Sun sweeps equal areas in equal intervals of time
AB and CD are distances covered by the planet in equal time i.e. after equal in- tervals of time, the positions of the planet starting from A a
Kepler’s third law : The square of its period of revolution around the Sun is directly proportional to the cube of the mean distance of a planet from the Sun.
Newton’s universal law of gravitation : All the above considerations including Kepler’s laws led Newton to formulate his theory of Universal gravity. According to this theory, every object in the Universe attracts every other object with a definite force. This force is directly proportional to the product of the masses of the two objects and is inversely proportional to the square of the distance between them.
Figure 1.5 shows two objects with masses m1 and m2 kept at a distance d from each other. Mathematically, the gravitational force of attraction between these two bodies can be written as
Here, G is the constant of proportionality and is called the Universal gravitational constant. The above law means that if the mass of one object is doubled, the force between the two objects also doubles. Also, if the distance is doubled, the force decreases by a factor of 4. If the two bodies are spherical, the direction of the force is always along the line joining the centres of the two bodies and the distance between the centres is taken to be d. In case when the bodies are not spherical or have irregular shape, then the direction of force is along the line joining their centres of mass and d is taken to be the distance between the two centres of mass.
From equation (2), it can be seen that the value of G is the gravitational force acting between two unit masses kept at a unit distance away from each other. Thus, in SI units, the value of G is equal to the gravitational force between two masses of 1 kg kept 1 m apart.
Why did Newton assume inverse square dependence on distance in his law of gravitation? He was helped by Kepler’s third law in this as shown below. Uniform circular motion / Magnitude of centripetal force Consider an object moving in a circle with constant speed. We have seen earlier that such a motion is possible only when the object is constantly acted upon by a force directed towards the centre of the circle. This force is called the centripetal force. If m is the mass of the object, v is its speed and r is the radius of the circle, then it can be shown that this force is equal to F = m v2 /r. If a planet is revolving around the Sun in a circular orbit in uniform circular motion, then the centripetal force acting on the planet towards the Sun must be F = mv2 /r, where, m is the mass of the planet, v is its speed and r is its distance from the Sun.
Thus, Newton concluded that the centripetal force which is the force acting on the planet and is responsible for its circular motion, must be inversely proportional to the square of the distance between the planet and the Sun. Newton identified this force with the force of gravity and hence postulated the inverse square law of gravitation. The gravitational force is much weaker than other forces in nature but it controls the Universe and decides its future. This is possible because of the huge masses of planets, stars and other constituents of the Universe.
Earth’ gravitational force Will the velocity of a stone thrown vertically upwards remain constant or will it change with time? How will it change? Why doesn’t the stone move up all the time? Why does it fall down after reaching a certain height? What does its maximum height depend on ? The earth attracts every object near it towards itself because of the gravitational force. The centre of mass of the earth is situated at its centre, so the gravitational force on any object due to the earth is always directed towards the centre of the earth. Because of this force, an object falls vertically downwards on the earth. Similarly, when we throw a stone vertically upwards, this force tries to pull it down and reduces its velocity. Due to this constant downward pull, the velocity becomes zero after a while. The pull continues to be exerted and the stone starts moving vertically downward towards the centre of the earth under its influence.
According to Newton’s law of gravitation, every object attracts every other object. Thus, if the earth attracts an apple towards itself, the apple also attracts the earth towards itself with the same force. Why then does the apple fall towards the earth, but the earth does not move towards the apple? The gravitational force due to the earth also acts on the moon because of which it revolves around the earth. Similar situation exists for the artificial satellites orbiting the earth. The moon and the artificial satellites orbit the earth. The earth attracts them towards itself but unlike the falling apple, they do not fall on the earth, why? This is because of the velocity of the moon and the satellites along their orbits. If this velocity was not there, they would have fallen on the earth.
Earth’s gravitational acceleration The earth exerts gravitational force on objects near it. According to Newton’s second law of motion, a force acting on a body results in its acceleration. Thus, the gravitational force due to the earth on a body results in its acceleration. This is called acceleration due to gravity and is denoted by ‘g’. Acceleration is a vector. As the gravitational force on any object due to the earth is directed towards the centre of the earth, the direction of the acceleration due to gravity is also directed towards the centre of the earth i.e. vertically downwards.
Variation in value of g A. Change along the surface of the earth : Will the value of g be the same everywhere on the surface of the earth? The answer is no. The reason is that the shape of the earth is not exactly spherical and so the distance of a point on the surface of the earth from its centre differs somewhat from place to place. Due to its rotation, the earth bulges at the equator and is flatter at the poles. Its radius is largest at the equator and smallest at the poles. The value of g is thus highest (9.832 m/s2 ) at the poles and decreases slowly with decreasing latitude. It is lowest (9.78 m/s2 ) at the equator. B. Change with height : As we go above the earth’s surface, the value of r in equation
(5) increases and the value of g decreases. However, the decrease is rather small for heights which are small in comparison to the earth’s radius. For example, remember that the radius of the earth is 6400 km. If an aeroplane is flying at a height 10 km above the surface of the earth, its distance from the earth’s surface changes from 6400 km to 6410 km and the change in the value of g due to it is negligible. On the other hand, when we consider an artificial satellite orbiting the earth, we have to take into account the change in the value of g due to the large change in the distance of the satellite from the centre of the earth. Some typical heights and the values of g at these heights are given in the following table.
C. Change with depth : The value of g also changes if we go inside the earth. The value of r in equation (5) decreases and one would think that the value of g should increase as per the formula. However, the part of the earth which contributes towards the gravitational force felt by the object also decreases. Which means that the value of M to be used in equation (5) also decreases. As a combined result of change in r and M, the value of g decreases as we go deep inside the earth.
Do you know ?
Weightlessness in space Space
travellers as well as objects in the spacecraft appear to be floating. Why does this happen? Though the spacecraft is at a height from the surface of the earth, the value of g there is not zero. In the space station the value of g is only 11% less than its value on the surface of the earth.
Thus, the height of a spacecraft is not the reason for their weightlessness. Their weightlessness is caused by their being in the state of free fall. Though the spacecraft is not falling on the earth because of its velocity along the orbit, the only force acting on it is the gravitational force of the earth and therefore it is in a free fall.
As the velocity of free fall does not depend on the properties of an object, the velocity of free fall is the same for the spacecraft, the travelers and the objects in the craft. Thus, if a traveller releases an object from her hand, it will remain stationary with respect to her and will appear to be weightless.

