Roman Numerals Problem Set 1 | Maharashtra State Board Class 5 Maths Solutions Chapter 1 Roman Numerals Problem Set 1
Question 1. Write all the numbers from 1 to 20 using Roman numerals.
Solution:
Question 2. Write the following numbers using international numerals.
[1] V
[2] VII
[3] X
[4] XIII
[5] XIV
[6] XVI
[7] XVIII
[8] IX
Solution:
[1] 5
[2] 7
[3] 10
[4] 13
[5] 14
[6] 16
[7] 18
[8] 9
Question 3. Fill in the empty boxes.

Answer:

Question 4. Write the numbers using Roman numerals.
[1] 9
[2] 2
[3] 17
[4] 4
[5] 11
[6] 18
Solution:
[1] IX
[2] II
[3] XVII
[4] IV
[5] XI
[6] XVIII
Question 5. In the table below, each given number is written in international numerals and then again in Roman numerals. If it is written correctly in Roman numerals, put ‘/’ in the box under it. If not, put ‘X’ and correct it.
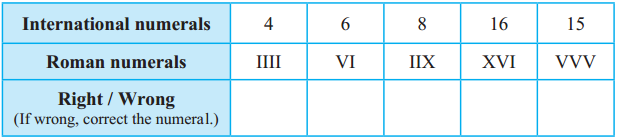
Answer: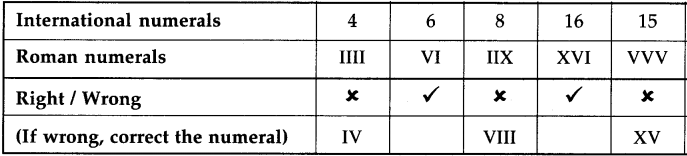
Something more : L, C, D and M are also used as Roman numerals.
Activity : Apart from clocks and watches, where else do we see Roman numerals?
The decimal system of writing numbers
It is not easy to read or write numbers using Roman numerals. It also makes calculations difficult. You have learnt to write numbers using the ten digits, 0 to 9. In that system, the value of a digit depends upon its place in the number. This system of writing numbers is called the ‘decimal system’.
Mathematicians of ancient India invented the decimal system of writing numbers and began to use it. Later, this system was accepted in all parts of the world because it was simple and convenient.
Roman Numerals Problem Set 1 Additional Important Questions and Answers
Question 1. Write all the numbers from 21 to 30 using roman numerals.
Solution:

Question 2. Write the following numbers using international numerals.
[1] XXV
[2] XXIX.
Solution:
[1] 25
[2] 29
Question 3. Fill in the empty boxes:
Solution:

Question 4. Write the numbers using Roman Numerals:
[1] 1
[2] 21
[3] 10
Solution:
[1] I
[2] XXI
[3] X
Question 5. In the table below, each given number is written in international numerals and then again in Roman numerals. If it is written correctly in Roman numerals put ‘S’ in the box under it. if not, put ‘x’ and correct it.
Solution:

Question 6. Write all the numbers from 31 to 40 using Roman numerals.
Solution:

Question 7. Write the following numbers using international numerals.
[1] VI
[2] XI
[3] XIV
[4] XVII
Solution:
[1] 6
[2] 11
[3] 14
[4] 17
Question 8. Fill in the empty boxes:
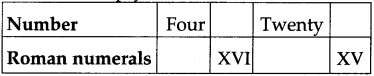
Four = IV, 16 = XVI, Twenty = XX, XV =15
Question 9. Write the numbers using Roman numerals in the given boxes.
[1] 3 [ ]
[2] 8 [ ]
[3] 13 [ ]
[4] 16 [ ]
Solution:
[1] III
[2] VIII
[3] XIII
[4] XVI
Question 10. State true or false of the following. If the statement is false then correct it in Roman numerals.
[1] 3 is written as IIV
[2] 14 is written as XIV
[3] 16 is written as XVI
[4] 19 is written as IXX
Solution:
[1] False [III]
[2] True
[3] True
[4] False [XIX]
Maharashtra Board Class 5 Maths Solutions Chapter 1 Roman Numerals Problem Set 1
Question 11. Write the answers Roman numerals.
[1] III + IV = [ ]
[2] IV + V = [ ]
[3] IX – X = [ ]
[4] VI + X = [ ]
[5] III + II = [ ]
[6] V + V = [ ]
[7] XXX + XX = [ ]
[8] L + L = [ ]
Solution:
[1] VII
[2] IX
[3] XIX
[4] XVI
[5] V
[6] X
[7] L
[8] C
Question 12. Match the columns:

Solution:
[1 – b],
[2 – a],
[3 – d],
[4 – c]
Maharashtra Board Class 5 Maths Solutions Chapter 1 Roman Numerals Problem Set 1
Question 13. Circle the correct international numeral of the following:
[1] XXIV
[a] 14
[b] 20
[c] 24
Solution:
[c] 24
[2] VIII
[a] 8
[b] 207
[c] 19
Solution:
[a] 8
[3] XXIX
[a] 31
[b] 29
[c] 20
Solution:
[b] 29
[4] XXVII
[a] 27
[b] 28
[c] 26
Solution:
[a] 27
Maharashtra Board Class 5 Maths Solutions Chapter 1 Roman Numerals Problem Set 1
Question 14. Circle the correct Roman numeral of the following:
[1] 36
[a] XXVI
[b] XXXVI
[c] XXXXVI
Solution:
[b] XXXVI
[2] 27
[a] XXXVI
[b] XXVII
[c] XXVI
Solution:
[c] XXVII
[3] 18
[a] XVIII
[b] XVI
[c] XVII
Solution:
[a] XVIII
[4] 605
[a]DCV
[b]CDV
[c] XXXXXV
Solution:
[a] DCV
Maharashtra Board Class 5 Maths Solutions Chapter 1 Roman Numerals Problem Set 1
Question 15. Put >, < or = in the box.
[1] CVI [ ] CLX
[2] CLXIX [ ] CLXXI
[3] XLIX [ ] XXXIX
[4] MMXVI [ ] MMXXVI
[5] LXX VII [ ] LVIII
[6] MCMXL [ ] MCMXLV
Solution:
[1] <
[2] <
[3] >
[4] <
[5] >
[6] <
Roman Numerals Problem Set 1 | Maharashtra State Board Class 5 Maths Solutions Chapter 1 Roman Numerals Problem Set 1
Geeta : This clock doesn’t have numbers. It has some
symbols instead.
Teacher : Yes, Geeta! These are Roman numerals. In Europe,
in the old times, Roman capital letters were used to write
numbers. That is why, they were called Roman numerals.
The letter ‘I’ was the symbol used for 1, ‘V’ for 5, and
‘X’ for 10.
In this method, there was no symbol for zero. Also, the value of a symbol did not
change with its place. There are certain rules for writing numbers using the Roman
numerals. Let us see how to write 1 to 20 using these rules and the symbols I, V and X.
Rule 1 : If either of the symbols I or X is written consecutively two or three times, their
sum total is the number they make.
Examples : II = 1 + 1 = 2 XX = 10 + 10 = 20 III = 1 + 1 + 1 = 3
Rule 2 : The symbols I or X can be repeated consecutively for a maximum of three times.
The numeral V is never repeated consecutively.
Rule 3 : When either I or V is written on the right of the symbol of a bigger number, its
value is added to the value of the bigger number.
Examples :
- VI = 5 + 1 = 6
- XI = 10 + 1 = 11
- XV = 10 + 5 = 15
- VII = 5 + 2 = 7
- XII = 10 + 2 = 12
- XVI = 10 + 5 + 1 = 16
- VIII = 5 + 3 = 8
- XIII = 10 + 3 = 13
Rule 4 : When I is written on the left of V or X, then its value is subtracted from the value
of V or X. However, the symbol I is not written more than once before V or X.
Examples : IV = 5 – 1 = 4 ,
IX = 10 – 1 = 9.
But, the number 8 is not written as IIX
14 = 10+1+1+1+1. However, we do not use the symbol I consecutively more than
3 times. Hence, we shall think of the number 14 as 10+4, instead. Then, using the
symbol IV for 4, we write 14 as XIV. Similarly, we shall think of the number 19 as
10 + 9 and write it as XIX.
Thus, to write the numbers from 1 to 20 in Roman numerals, we first distribute a given
number into groups of 10, 5 and 1 and then apply the rules given above.
Thus,
- 12 = 10 + 1 + 1 = XII,
- 7 = 5 + 1 + 1 = VII,
- 18 = 10 + 5 + 3 = XVIII

